
-
¿Cuál es la expresión algebraica del largo del terreno? -
¿Cuál es la expresión algebraica del ancho del terreno? -
¿Cuál es el perímetro del terreno? -
¿Cuál es el área del terreno? -
¿Cuáles expresiones representan el área de todo el terreno? -
¿Cuál será el perímetro de la casa? -
¿Cuál será el área de la casa? -
¿Cuál es el área del terreno y de la casa si x =6? -
¿Cuánto mide el ancho de un terreno rectangular que mide 2X de largo y su área es de ? -
Cómo calculas el área de una figura si sus dimensiones están dadas en forma de expresión algebraica?
Todas estas preguntas las vamos a resolver con las herramientas de las operaciones algebraicas a través de Suma y Multiplicación de expresiones algebraicas.




 Porque según la definición de multiplicar, el signo del producto tiene que ser respecto del signo del multiplicando lo que el signo de multiplicador es respecto de la unidad positiva, pero en este caso, el multiplicador tiene el mismo signo que la unidad positiva; luego, el producto necesita tener el mismo signo que el multiplicando, pero el signo de multiplicando es +, luego, el signo del producto será +.
Porque según la definición de multiplicar, el signo del producto tiene que ser respecto del signo del multiplicando lo que el signo de multiplicador es respecto de la unidad positiva, pero en este caso, el multiplicador tiene el mismo signo que la unidad positiva; luego, el producto necesita tener el mismo signo que el multiplicando, pero el signo de multiplicando es +, luego, el signo del producto será +.
 Porque teniendo el multiplicador el mismo signo que la unidad positiva, el producto necesita tener el mismo signo que el multiplicando, pero éste tiene -, luego, el producto tendrá -.
Porque teniendo el multiplicador el mismo signo que la unidad positiva, el producto necesita tener el mismo signo que el multiplicando, pero éste tiene -, luego, el producto tendrá -.




























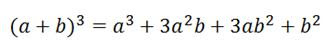

 El factor común es:
El factor común es:  cada término del polinomio se divide entre el factor común y se tiene:
cada término del polinomio se divide entre el factor común y se tiene:







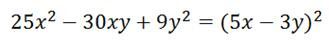
 Un trinomio de la forma x2+bx+c es cuadrado perfectos si el término bx es el doble producto de las raíces cuadradas de los otros dos.
Un trinomio de la forma x2+bx+c es cuadrado perfectos si el término bx es el doble producto de las raíces cuadradas de los otros dos.

